자바 백준 9506번
브론즈 1
https://www.acmicpc.net/problem/9506
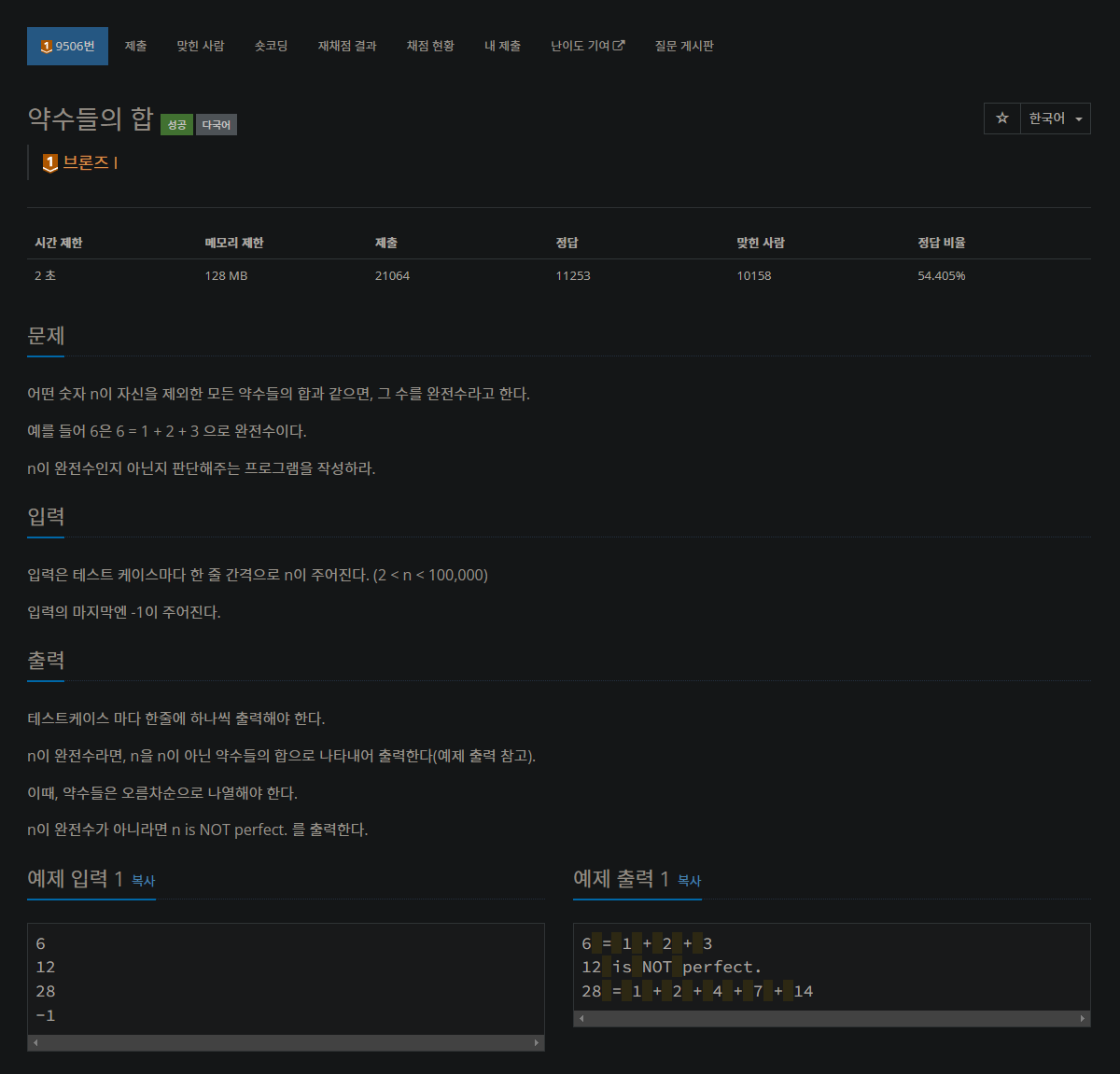
9506번: 약수들의 합
어떤 숫자 n이 자신을 제외한 모든 약수들의 합과 같으면, 그 수를 완전수라고 한다. 예를 들어 6은 6 = 1 + 2 + 3 으로 완전수이다. n이 완전수인지 아닌지 판단해주는 프로그램을 작성하라.
www.acmicpc.net
문제 보기
분류: 수학, 구현, 정수론
문제 풀기
while loop를 이용하여 n을 지속적으로 입력받는다.
입력받은 n이 완전수인지 확인한다.
완전수는 for loop와 약수의 정의를 통해 약수를 찾고 그 수들을 모두 누적합하여 확인한다.
완전수 인지 아닌지 조건 분기하여 결과를 형식에 맞게 출력한다.
코드 보기
import java.util.Scanner;
import java.util.List;
import java.util.ArrayList;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n; // 변수 n 지정.
// 입력된 n을 완전수인지 확인하고 결과를 분기하여 출력하는 while loop.
while ((n = sc.nextInt()) != -1) { // 매 loop 마다 n을 입력받는다. -1이 입력되었을땐 종료.
// n이 완전수 일때.
if (isPerfectNumber(n)) {
// 약수 가져옴.
List<Integer> divisors = getDivisors(n);
// 결과 출력 형식.
System.out.print(n);
System.out.print(" = ");
for (int i = 0; i < divisors.size() - 1; i++) {
System.out.print(divisors.get(i) + " + ");
}
System.out.println(divisors.get(divisors.size() - 1));
}
// n이 완전수 아닐때.
else {
// 결과 출력 형식.
System.out.println(n + " is NOT perfect.");
}
}
}
private static boolean isPerfectNumber(int n) {
int sum = 0;
// 약수의 정의로 수를 찾고 누적합. n/2까지 확인.
for (int i = 1; i <= n / 2; i++) {
if (n % i == 0) {
sum += i;
}
}
return sum == n; // 약수들의 합 sum이 n과 같으면 true.
}
private static List<Integer> getDivisors(int n) {
List<Integer> divisors = new ArrayList<>();
// 약수의 정의로 수를 찾고 list에 저장. n/2까지 확인.
for (int i = 1; i <= n / 2; i++) {
if (n % i == 0) {
divisors.add(i);
}
}
return divisors;
}
}
'공부하기 > 백준' 카테고리의 다른 글
| [Java] 백준 풀기 15439 - 베라의 패션 (0) | 2023.07.03 |
|---|---|
| [Java] 백준 풀기 2581 - 소수 (0) | 2023.07.02 |
| [Java] 백준 풀기 2745 - 진법 변환 (0) | 2023.06.30 |
| [Java] 백준 풀기 2566 - 최댓값 (0) | 2023.06.29 |
| [Java] 백준 풀기 3003 - 킹, 퀸, 룩, 비숍, 나이트, 폰 (0) | 2023.06.28 |