파이썬 백준 3053번
브론즈3
https://www.acmicpc.net/problem/3053
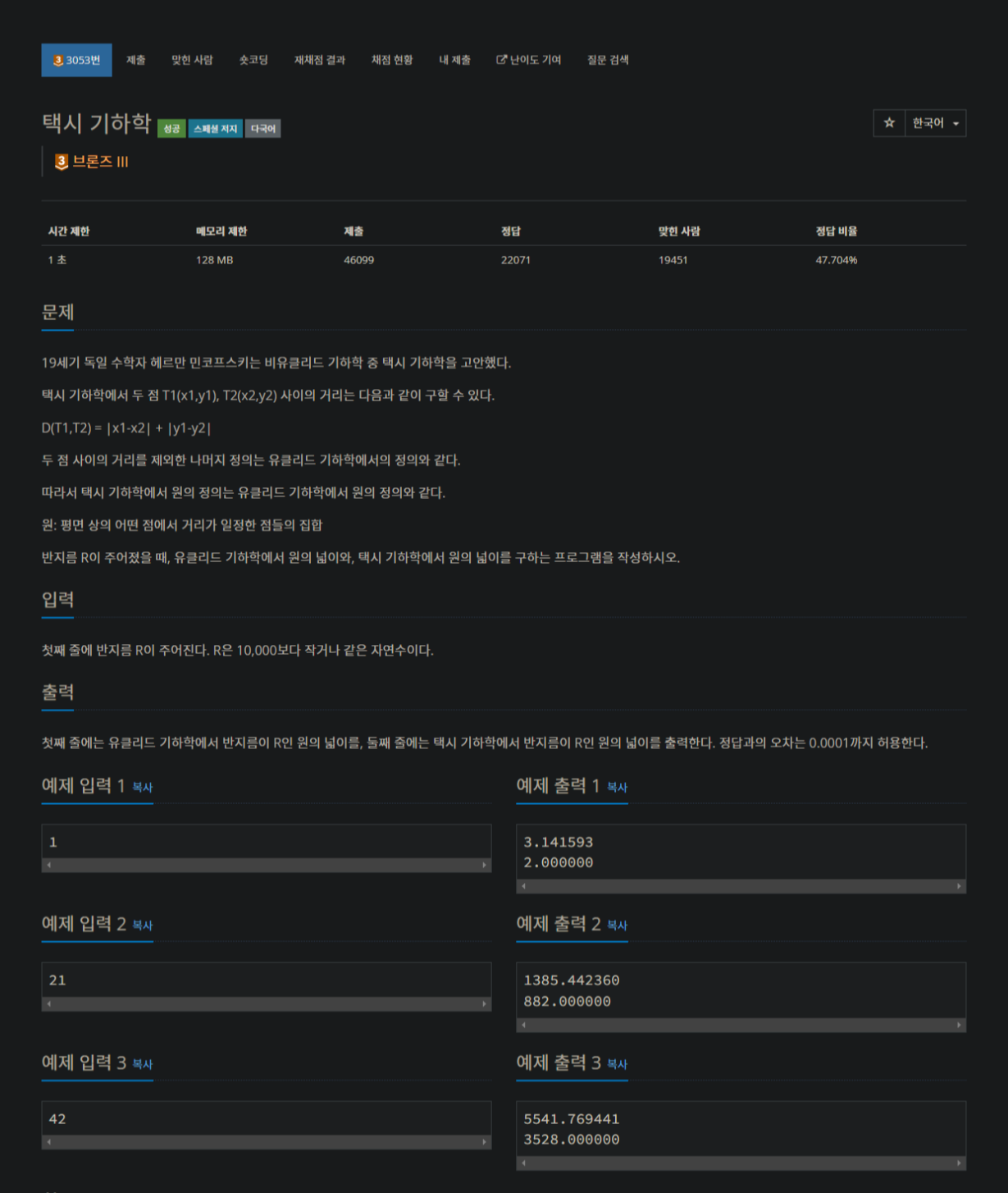
3053번: 택시 기하학
첫째 줄에는 유클리드 기하학에서 반지름이 R인 원의 넓이를, 둘째 줄에는 택시 기하학에서 반지름이 R인 원의 넓이를 출력한다. 정답과의 오차는 0.0001까지 허용한다.
www.acmicpc.net
문제 보기
분류: 기하 1 단계, 수학, 기하학
문제 풀기
당연하겠지만 택시 기하학이 무엇인지 이해하는 게 이 문제의 포인트인 것 같다. 수학적 무언가를 요구한다기 보다는..
그리고 필요한 건 원의 정의
"원은 평면 위의 한 점에 이르는 거리가 일정한 평면 위의 점들의 집합으로 정의되는 도형이다."
유클리드 기하학에서 일정한 거리의 점들을 모아놓으면 이미 잘 알고 있는 동그란 원이다. 하지만 택시 기하학에서 일정한 거리의 점들을 모으면 그 모습이 달라진다.
일단 빠른 이해를 하기 위해 택시 기하학을 그림으로 설명하는 위키를 보면 아래와 같다.
https://ko.wikipedia.org/wiki/%EB%A7%A8%ED%95%B4%ED%8A%BC_%EA%B1%B0%EB%A6%AC
맨해튼 거리 - 위키백과, 우리 모두의 백과사전
위키백과, 우리 모두의 백과사전. 맨해튼 거리(Manhattan distance, 혹은 택시 거리, L1 거리, 시가지 거리,Taxicab geometry)는 19세기의 수학자 헤르만 민코프스키가 고안한 용어로, 보통 유클리드 기하학
ko.wikipedia.org
가로와 세로 길로만 움직여 갈 수가 있어 두 점의 최단거리 모양이 90도를 꺾어 움직이는 형태가 된다.
택시 기하학에서 90도 꺽어 움직이는 형태로 원의 정의를 표현해 보면 아래와 같다.

2차원 평면에 점이 위치할 수 있는 좌표들을 4개의 다른 경우로 표현해 보았다.
1 사분면에서만 같은 거리의 점들을 생각해 보면,
왼쪽 위의 경우는 단위 모눈이 크기 때문에 중심에서 오른쪽과 위쪽에만 빨간 점이 위치한다.
오른쪽 위의 경우 절반의 모눈이 더 추가되어 같은 거리에 위치할 수 있는 점들은 왼쪽 2칸, 위쪽 2칸 그리고 왼쪽 1칸 위쪽 1칸에 위치할 수 있다.
이를 더 확장하여 왼쪽 아래의 그림이 만들어지고, 무수히 많아지면 오른쪽 아래의 그림과 같이 일정한 거리의 점들은 대각선 형태를 띠게 된다.
따라서, 택시 기하학에서 원의 정의를 그려본다면 마름모 형태를 띠고, 원의 넓이도 마름모의 넓이로 계산될 수 있다.
이제 문제에서 요구하는 유클리드 기하학에서 원의 넓이와 택시 기하학에서 원의 넓이를 코드로 표현하면
EG_area = math.pi * r ** 2
TG_area = ((2 * r) ** 2) / 2
와 같다.
코드 보기
import sys
inputdata = sys.stdin.readline
import math
def fnEuclideanGeometry(r):
# pi = 3.141592653589793
# pi = math.acos(-1)
EG_area = math.pi * r ** 2
return round(EG_area, 6)
def fnTaxicabGeometry(r):
TG_area = ((2 * r) ** 2) / 2
return round(TG_area, 6)
if __name__ == "__main__":
r = int(inputdata().strip())
EG_area = fnEuclideanGeometry(r)
print(EG_area)
TG_area = fnTaxicabGeometry(r)
print(TG_area)
'공부하기 > 백준' 카테고리의 다른 글
| [Python] 백준 풀기 2675 - 문자열 반복 (0) | 2022.10.28 |
|---|---|
| [Python] 백준 풀기 11651 - 좌표 정렬하기 2 (0) | 2022.10.27 |
| [Python] 백준 풀기 2563 - 색종이 (1) | 2022.10.25 |
| [Python] 백준 풀기 7568 - 덩치 (0) | 2022.10.24 |
| [Python] 백준 풀기 11650 - 좌표 정렬하기 (0) | 2022.10.23 |